Egy szórakoztató matematikai feladat megoldása adta az ötletet eme cikk megírásához. Ez a probléma legjobban a bűvös négyzetekről szóló feladatokhoz hasonlít, egy sokszögekből álló gráf (lényegében egy ún. Dávid-csillag) csúcspontjait úgy kell "súlyozni" (föléjük nemnegatív [egész] számokat írni), hogy az egy egyenesre eső csúcsok súlyainak összege mindig S=26 legyen.
A feladatnak rövidebb és hosszabb megoldását közöljük. A hosszabb megoldás bonyolultabb, ámde tanulságosabb is, mert kapcsolatban van a halmazrendszerek kombinatorikájának elméletével, így a feladat megoldásával foglalkozó tanulók e példa kapcsán esetleg először ismerkednek meg a blokkrendszerekre vonatkozó kombinatorikus fogalmakkal és tételekkel. Foglalkozunk a feladat különféle általánosításaival is, melyekben a pontok száma hat helyett nyolc, tíz, ... stb., illetve amelyekben S nem feltétlenül 26.
A feladat a következő:
Adott egy "Dávid-csillag": ez egy "vízszintes" alapú szabályos háromszögnek és (köréírható körének) középpontja körüli 180o-os elforgatottjának uniója. Másképpen is fogalmazhatunk: egy "vízszintes" oldalú szabályos hatszög oldalait hosszabbítsuk meg addig, mígnem metszik egymást, képezzük a hatszög eredeti és meghosszabított oldalainak unióját.
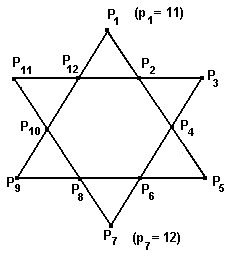
A következő ábrát kapjuk:

Tekintsük azon síkbeli pontokat, amelyekben valamely két (különböző) háromszögoldal metszi egymást: az ábrán ezeket P1, P2, ..., P12 jelöli. Minden Pi ponthoz hozzárendelünk egy pi∈ℕ+ pozitív egész számot. Keressünk olyan hozzárendelést, amelyre p1 = 11 és p7 = 12; és bármely négy, egy egyenesre eső ponthoz rendelt számok összege épp 26, továbbá a pi számok (i∈{1, 2, ..., 12}) páronként különbözőek!
Röviden: "töltsük ki az ábrát" úgy számokkal, hogy minden "sorban" (az egy oldalegyenesre eső pontokban) 26 legyen a számok összege.
Többféle irányban elindíthatjuk gondolatmenetünket, a heurisztika szerteágazó csápjaival ragadhatjuk meg s szedhetjük ízekre a problémát. És ha a kedves Olvasó esetleg, nem tudván, mi az a "heurisztika", ennek mibenléte felől érdeklődne; reméljük e kis írásból némi segítséget kap kérdése megválaszolásához.
Javaslom az Olvasónak (ha még nem ismeri a feladat megoldását), hogy mielőtt továbbhaladna, próbálja meg legalább negyed-fél órán át a fenti feltételeknek megfelelően kitölteni az ábrát, megoldani a rejtvényt! De talán akkor is hasznos lesz a következőket elolvasni, ha ismer egy megoldást, de "véletlenül", próbálgatások útján jött rá.
Hogyan lehet rájönni egy probléma megoldására "isteni sugallat" nélkül, pusztán a birtokunkban lévő tudásra alapozva? Lehetséges ez? Vagy talán úgy hangzik helyesen e kérdés, hogy milyen módszereket tudunk adni az "isteni sugallatok" célzott elérésére? És ha ezt esetleg nem is tudjuk megválaszolni mindezeket, még mindig marad a kérdés: hogyan lehet elmagyarázni egy "isteni sugallatot" olyanoknak, akik ilyenekkel (még) nem rendelkeznek? Persze anélkül, hogy a sajnos sokat használt, "vegyük észre"-típusú, teljesen fölösleges, sőt alighanem káros fordulatokat használnánk, mely magát a "sugallatot" természetes és elengedhetetlen kiindulópontként kezeli, holott az iskolának épp a "sugallat" elérését kellene megtanítania, nem pedig csupán azt, mit kell tenni, ha már megvan.
A heurisztika első számú szabálya, hogy először is próbáljunk abból kiindulni, amit ismerünk. Mit ismerünk? Mi van adva? – kérdezné Pólya György, a modern heurisztika (a kreatív gondolkodás, a problémamegoldás és a felfedezések mibenlétét és célszerű módjait vizsgáló tudományág) egyik atyja.
Számszerűen ismerünk két számot, a továbbiakban "súlyt": a 11-et és 12-t. Ezenkívül ismerjük minden sorban a "súlyok" összegét, a 26-ot. A feladatunk az, hogy "szétosztogassuk" e súlyokat a jelentkező 12 db pont között.
Ezért a második ismeret, a súlyok összegének ismerete - érezhetően? beláthatóan? - sokkal nagyobb információtartalommal bír. Valóban, ez viszonylag kis szám, így azokban a sorokban, ahol egy-egy súly értéke már adva van, egy viszonylag kis számot kell négy pozitív egész összegére bontani. Ez még mindig elég sok próbálkozást igényelhet. Abban a szerencsés helyzetben vagyunk azonban, hogy az adott súlyok elég nagyok, majdnem 26/2 nagyságúak, így egy még kisebb számot kell csak nem sokkal (eggyel) kevesebb pozitív egész összegére felbontani.
Egy gondolkodtató kérdés: mikor lenne könnyebb megoldani ezt a feladatot? Ha a súlyok összegét nem ismernénk, csak azt tudnánk, hogy a súlyok (páronként) különbözőek, és minden sorban a súlyok összege ugyanakkora, de ismernénk két súlyt (javasolom az Olvasónak, gondolkozzon el pár percig ezen a feladatváltozaton is, és látni fogja, hogy nehéz). Vagy ha a páronként különböző súlyok összegét ismernénk, de a segítségként megadott két súly értékét nem? Az Olvasó látni fogja, hogy a feladat eme utóbbi változata lényegében nem vagy nem sokkal nehezebb, mint az a feladat, amit most próbálunk megoldani.
Erről az észrevételről nem látszik, hogy végül is célhoz vezetne. Igaz, hogy p1+p2+p4+p5 = 26 és p1 = 11 miatt p2+p4+p5 = 26-11 = 15, hasonlóan p3+p4+p6+p7 = 26 és p7 = 12 miatt p3+p4+p6 = 14; vagyis 15-nek és 14-nek olyan háromtagú összegekre bontását (partícióját) kell megtalálnunk, amelyekben van egy közös p4 tag, de ez még mindig elég sok próbálgatási lehetőséget jelent (p4 1-től 10-ig változhat, ekkor pl. p3+p6 13-tól 3-ig változhat, de ha p4 esetleg kicsi, akkor ez még mindig több mint tíz lehetőséget jelent - és ez csak p4 egy rögzített értéke mellett, de hát p4 is változhat, elvileg tízféle értéket is felvehet; vagyis a variációk száma nagyon durván 130; és ez csak eme sor kitöltési lehetőségeinek becsült száma, ha egy másik sornak csak 10 kitöltési lehetősége marad, akkor is 1300 variánst kell kipróbálni!).
Írjunk fel egyenletrendszert? Tizenkét ismeretlenes egyenletrendszer ... - hmm, egy MAPLE, DERIVE vagy hasonló program valószínűleg pillanatok alatt megoldaná, de ilyet használni most definíció szerint csalás! Lineáris programozás? Gráfelméleti tételek? Most hagyjuk egyenlőre a komoly módszereket, ez egy elemi feladat, hátha van elemi megoldása is.
Minthogy kevés lépésben nem tudjuk azonnal láthatóan "lebontogatni" a súlyokat (legalábbis kevesek képesek erre, és azok is valószínűleg sokat gyakorolták), a probléma eléggé ellenáll a "szintetikus" megoldási kísérleteknek, próbáljuk inkább globálisan, "analitikusabban" szemlélni. Egyáltalán van valami, amit ezen kívül ki tudunk számolni? Számításba vettünk minden lényeges adatot, kikötést, összefüggést? Az összes súly összegét pl. még viszonylag könnyen ki tudjuk számolni. 6 sokszögoldal van az ábrán, mindegyiken négy pont, amelyek súlyainak összege mindig 26. Az is látható, hogy minden pont, azaz minden súly pontosan két sokszögoldalon van rajta. Tehát a súlyok összege 6·26/2 = 78. Ez az esetleg haszontalannak látszó észrevétel fogja a megoldáshoz vezető utat elindítani.
Tehát a megoldás: minden sorban a súlyok összege 26, minden pont, azaz minden súly pontosan két sokszögoldalon van rajta; így a súlyok összege 6·26/2 = 78.
Segít ez valamit? Talán ha "észrevesszük", hogy 78 = 6·26/2 = 6·2·13/2 = 12·13/2. Ugyanis erről "eszünkbe juthat" az 1+2+...+11+12 = 12·13/2 képlet, hiszen általában is 1+2+...+(n-1)+n = n·(n+1)/2. Nem valószínű, bizonyosnak mindenesetre egyáltalán nem bizonyos, hogy ez "csak úgy" az eszünkbe jut, ugyan miért is jutna, de nem is lehetetlen. Mindenesetre eredeti kérdésünk az volt, el tudjuk-e magyarázni a feladat megoldását a "vegyük észre" szó használata nélkül.
Példa egy módra, hogy lyukadhatunk ki ide:
A súlyok összege 78 – ez annyit jelent, hogy 78-at kell 12 db. különböző pozitív egész szám összegére felbontani. Ez pedig annyit jelent, hogy "átlagosan" egy szám 78/12 = 13/2=6.5 nagyságú. Ez nyilván korlátot jelent az egyes súlyok nagyságára nézve, hiszen pl. nem lehet egyik súly sem 78 nagyságú.
Adjunk tehát alsó és felső becslést a súlyok nagyságára nézve: mekkora lehet a legnagyobb, illetve a legkisebb súly? Az alsó becslést könnyebb megadni: nyilván 1-nél kisebb egyik súly sem lehet. Legyen tehát az első súly 1. Mekkora lehet az ezt követő legkisebb súly: már nem lehet 1 (páronként különbözőek a súlyok), de lehet 2. És így tovább. Vagyis eljutunk az 1, 2, .., 11, 12 számsorhoz. De vajon eléggé éles-e ez a becslés, lehet-e a súlyok összege kb. 78; vagy ez a becslés túl alacsony számot szolgáltat a súlyok összegére? Nézzük csak: ha átlagosan egy szám 6.5, akkor ez a becslés valószínűleg többé-kevésbé pontos. És valóban annyi:
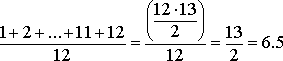
Sőt! Minthogy 1+2+...+11+12 = 12·13/2 = 78, ez az összeg pontosan 78! Azt kaptuk, hogy ha feladatunk megoldható, létezik a keresett súlyrendszer, az csak az 1, 2, ..., 12 számsor lehet: belátható, hogy bármelyik súlyt növelve ugyanis már túl nagy lesz a súlyok összege, csökkentve pedig vagy lesz két egyenlő súly, vagy ami még rosszabb, lesz nempozitív súly. Ez utóbbi állítás részletesebb igazolását az Olvasóra bízzuk.
Lényegében készen is vagyunk: a megoldás hátralévő részében megpróbáljuk kitölteni ábránkat az 1, 2, ..., 12 számsorral. Valójában két szám már el van helyezve, így csak az 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 számok elhelyezésére van szükség.
Ezt lényegében próbálgatással oldjuk meg, de ügyelünk arra, hogy ez szisztematikus (áttekinthető) és célirányos legyen.
Több vagy kevesebb próbálkozás után rájöhetünk, hogy az ábrát még mindig nehéz kitölteni! Több lehetőségünk van, de pl. célszerűen először a nagy számokat próbáljuk elhelyezni a táblázatban. A probléma még így is túl nyílt lesz, bár sok lehetőséget "kilövünk", a lehetőségek száma még így is 10! nagyságrendű.
A feladat az, hogy számokat írjunk bizonyos helyekre. Két kérdésre kell ekkor válaszolnunk: a) mit írjunk? b) hová írjuk?
Célszerű először is a legnagyobb számok elhelyezésével próbálkozni. Ugyanis ha egy minél nagyobb számot elhelyezünk valahová, akkor azokban a sorokban már csak 26-nál minél kisebb számot kell összegekre bontani: és kis számok összegekre bontása sokkal kevesebb féleképp lehetséges.
Célszerű továbbá úgy elhelyezni ezen számokat, hogy minél kevesebb lehetőség maradjon a többi szám elhelyezésére, azaz lehetőleg olyan sorokba írni őket, amelyben már van foglalt elem. Ekkor ugyanis már csak két vagy kevesebb nem ismert értékű súly marad a sorban, melyek összege 26 ("nagy szám") = ("kis szám"), és kis számot csak viszonylag kevés féleképp lehet kevés szám összegére bontani. Ezért ha más ötletünk nincs, a legokosabb, amit tehetünk, hogy a p4 vagy a p10 súlynak próbálunk meg értéket adni, mivel ezek két olyan sorban is benne vannak, ahol már van kitöltött elem. Az is látható, hogy az ábra elég szimmetrikus, vagyis mindegy, melyik ponttal foglalkozunk a kettő közül. Legyen ez a P4 pont.
Tegyük hát fel, hogy p4 = 10 - ekkor p2+p5 = 26-(11+10) = 26-21=5. Továbbá p3+p6 = 26-(12+10) = 26-22 = 4. Márpedig 4-et és 5-öt csak a következőképp lehet két szám összegére bontani, ha a tagok az 1, 2, .., 9, 10 számsor különböző elemei: 4 = 1+3, 5 = 1+4 = 2+3. Szükségképp 4 = 1+3, de ekkor már 5-öt nem tudjuk felbontani, mert mindkét felbontás egyik tagja már "foglalt". Ennélfogva p4 10. Hasonlóan (a szimmetria miatt) p10 10.
Hasonlóan belátható p4 9,8,7; sőt még p4 6 is, és persze ugyanúgy p10 9,8,7,6.
Valójában ennek belátására sincs szükségünk: most már elég kevés próbálkozással az ábra kitölthető. Minthogy p4 10, de feltehető (a szimmetria miatt), hogy (p2-10)(p3-10)(p5-10)(p6-10) = 0, egyszerűen megpróbáljuk kitölteni az ábra jobb oldalát. Célszerű feltenni, hogy p3 = 10 vagy p6 = 10. Ugyanis ekkor a 12 súlyt tartalmazó sorba kerül a 10, és eme sorban 26-(12+10) = 26-22 = 4-et kell két szám összegeként előállítani, ami csak egyféleképp lehetséges: 4=1+3. Ha a másik, 11-et tartalmazó sorban helyeznénk el 10-et (a P2 v. P5 pontokban), akkor 26-(11+10) = 26-21 = 5-öt kell két szám összegére bontani, de ez kétféleképp is lehetséges: 5 = 1+4 = 2+3.
Tegyük hát fel, hogy p3 = 10. Ekkor p4+p6 = 26-(12+10) = 4 = 1+3.
Ha p4 = 3, akkor p6 = 1; ekkor p2+p5 = 26-(11+3) = 26-14 = 12. De az 1, 2, ..., 10 súlyok fel nem használt számai közül, a {2, 4, 5, 6, 7, 8, 9} számok közül kettő különböző segítségével 12 csak néhányféleképp állítható elő. A 12 = 1+11 = 2+10 = 3+9 = 4+8 = 5+7 felbontások közül az első három foglalt számokat tartalmaz, marad 12 = 4+8 = 5+7. Ekkor p4 = 3 miatt csak p6 = 1 lehet, és emiatt nem lehet p5 = 4 vagy p5 = 5. Ellenben ha p5 = 5, a P5P6P8P9 vízszintes sorban p8+p9 = 26-(p5+p6) = 26-6 = 20, vagy, ha p5 = 4, p8+p9 = 26-5 = 21, ám 20 és 21 nem állítható elő az 1, 2, ..., 10 súlyokból kettő összegeként, legfeljebb 10+9 = 19 (eme észrevétel segítségével lehet egyébként belátni, hogy p4 9,8,7). Tehát két lehetőségünk van: vagy p5 = 8, vagy p5 = 7. Ha p5 = 8, akkor p2 = 26-(11+8+3) = 26-22 = 4. A P5P6P8P9 vízszintes sorban ekkor p8+p9 = 26-(p5+p6) = 26-(8+1) = 26-9 = 17. A 17-et kéne a maradék fel nem használt súlyokból, a {2, 5, 6, 7, 9} halmazból előállítani. Ez nem lehetséges: most már csak maximum 9+7 = 16 állítható elő. Kiderült tehát, hogy p5 8, azaz p5 = 7. Ekkor p2 = 26-(11+7+3) = 26-21 = 5. A P5P6P8P9 vízszintes sorban ekkor p8+p9 = 26-(p5+p6) = 26-(7+1) = 26-8 = 18. A 18-at kéne a maradék fel nem használt súlyokból, a {2, 4, 6, 8, 9} halmazból előállítani. Ez nem lehetséges: most már csak maximum 9+8 = 17 állítható elő. Kiderült tehát, hogy p57. Ez azt is jelenti, hogy p4 = 3 nem lehetséges.
Azaz ha p3 = 10, akkor szükségképp p4 = 1 és p6=3. Ekkor p2+p5 = 26(11+1) = 26-12 = 14. Érvényes 14 = 1+13 = 2+12 = 3+11 = 4+10 = 5+9 = 6+8. A szóba jövő felbontások 5+9 és 6+8. De nem lehet p5 = 5 és p5 = 6. Ugyanis ezen esetekben a P5P6P8P9 vízszintes sorban p8+p9 26-(3+5) = 18, vagy 26-(3+6) = 17. Ezen számok azonban nem állíthatóak elő a maradék {2, 4, 6, 7, 8} illetve {2, 4, 5, 7, 9} halmazokból: az előállítható maximális számok 7+8 = 15 illetve 7+9 = 16. Így most is két lehetőségünk van: vagy p5 = 9 és p2 = 5, vagy p5 = 8 és p2 = 6. A második eset lehetetlen: a P3P2P12P11 vízszintes sorban ekkor p11+p12 = 26(p2+p3) = 26(6+10) = 26-16 = 10. 10-et kellene az A={2, 4, 5, 7, 9} halmazból előállítani. Ez nem lehetséges: 10 = 1+9 = 2+8 = 3+7 = 4+6 összes lehetséges felbontása tartalmaz egy-egy elemet az A halmazon kívülről.
Így aztán p2 = 5 és p5 = 9. Ebből kiszámolható p11+p12 = 26(10+5) = 11 és p8+p9 = 26(3+9) = 14. A maradék súlyok halmaza B = {2, 4, 6, 7, 8}. Ebből 11 egyféleképp állítható elő: 11 = 4+7 = p11+p12. A maradék számok halmaza B’ = {2, 6, 8}. Ebből 14 csak egyféleképp állítható elő: 14 = 6+8 = p8+p9. A maradék számok halmaza C={2}. Ebből következően ez lesz az egyetlen, eddig még nem vizsgált p10 = 2 súly értéke.
Most már könnyen rájövünk, hogy p11 = 4 és p8 = 8. Ugyanis a P7P8P10P11 sorban p11+p8 = 26-(p10+p7) = 26-(2+12) = 12. A p11 súly vagy 4, vagy 7, a p8 súly vagy 6, vagy 8. Ekkor p11+p8 = 12 = 8+48+7,6+4,6+7. Így már ki tudjuk az ábrát tölteni:
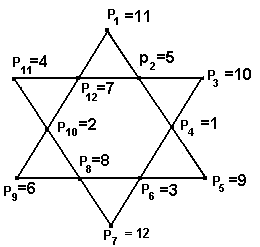
Ezzel e feladatot megoldottuk. Ezen kívül biztosan van ennek az ábrának még egy többé-kevésbé különböző kitöltése: ti. a fenti ábra "tükörképe" a P1P7 egyenesre (úgy értve, hogy a súlyokat tükrözzük, de a pontok maradnak). De most már bárki könnyedén, igaz, némi munkával kipróbálgathatja, hogy a fenti feladattól teljességgel különböző, a fenti ábrára nem szimmetrikus megoldások is léteznek.